クラスタリング

クラスタリングは、同じグループ内のオブジェクトが他のグループ内のオブジェクトよりも互いに類似するようにオブジェクトのセットをグループ化するタスクです。これは探索的データ分析の主なタスクであり、統計データ分析の一般的な手法であり、多くの分野で広く使用されています。

クラスタリング自体は特定のアルゴリズムではなく、クラスターを構成するものとそれらを効率的に見つけるさまざまなアルゴリズムがあります。

クラスタリングのアルゴリズム

クラスタリングの手法の一例と特徴をまとめています。

メソッド名	パラメーター	スケーラビリティ	使用事例	ジオメトリ
K-Means	クラスターの数	非常に大きいn_samples、中程度のn_clustersをMiniBatchコードを用いてスケールする	一般的に使用できる方法で、均一なクラスターサイズ、フラットジオメトリ、クラスターが多すぎない場合に有効	ポイント間の距離
Mean-shift	bandwidth	n_samplesに対してスケーラブルでない	多くのクラスターや不均一なクラスターサイズ、非平坦なジオメトリに対して有効	ポイント間の距離
Affinity Propagation	ダンピング、サンプルプリファレンス	n_samplesに対してスケーラブルでない	多くのクラスターや不均一なクラスターサイズ、非平坦なジオメトリに対して有効	グラフの距離（例：最近傍グラフ）
Spectral clustering	クラスターの数	中程度のn_samples、小程度のn_clusters	中程度のクラスター、均一なクラスターサイズ、非平坦なジオメトリジオメトリ、トランスダクティブで有効	グラフの距離（例：最近傍グラフ）

K-Means

今回はK-Meansというクラスタメンバー間の距離に着目した手法を学んでいきます。 K-Meansでは、クラスターの数を指定する必要があります。多数のサンプルに対応し、さまざまな分野の幅広いアプリケーション分野で使用されています。

inertiaについて

inertiaという単語が解説の中で出てくるのですが、Google翻訳では慣性と訳されてイメージがつかみにくい人もいるかと思います。 Scikit-learnのK-Meansの記事では、K-Meansのアルゴリズムの目的を、以下のように説明しています。

The K-means algorithm aims to choose centroids that minimise the inertia, or within-cluster sum-of-squares criterion: $$ \sum_{i=0}^{n}\min_{\mu_j \in C}(||x_i - \mu_j||^2) $$

K-Meansはinertiaを最小化する重心、またはクラスター内の二乗和基準を選択することを目的としています。ここでいうinertiaとは慣性モーメント（moment of inertia）と理解するとイメージがつきやすいと思います。慣性モーメントは、中心のとり方によってその値が変わり、中心として系の重心をとったとき、慣性モーメントは最小となります。

inertiaは値が小さいほどよく、ゼロが最適であることがわかっています。ですが、正規化されたメトリックではありません。非常に高次元の空間では、ユークリッド距離が膨らむ傾向があります（次元の呪い）。高次元のクラスタリングをK-Meansで行う場合は、クラスタリングの前に主成分分析などの次元削減を行うことで計算を高速化できます。

sklearn.cluster.KMeans

sklearnで実装されているKMeansは以下のようにパラメータを設定できます。

class sklearn.cluster.KMeans(n_clusters=8, *, init=‘k-means++’, n_init=10, max_iter=300, tol=0.0001, verbose=0, random_state=None, copy_x=True, algorithm=‘auto’)

パラメータ

メソッドに使用するパラメータは以下のようになっています。

パラメータ名	デフォルト	説明
n_clustersint	default=8	クラスターの数と生成する重心の数。
init	{‘k-means++’, ‘random’}, callable or array-like of shape (n_clusters, n_features), default=’k-means++’	‘k-means ++’：収束を高速化するための方法、‘random’：n_clusters最初の重心をランダムに設定する。
n_initint	default=10	異なる重心シードを使用してk-meansアルゴリズムが実行される回数。最終結果はinertiaがn_initの中で最良のものになる。
max_iterint	default=300	1回の実行でのk-meansアルゴリズムの最大反復回数。
tolfloat	default=1e-4	収束を宣言するための2つの連続した反復のクラスター中心の差のフロベニウスノルムに関する相対的な許容誤差。
verboseint	default=0	図心初期化の乱数生成を決定します。
random_stateint	RandomState instance or None, default=None	冗長モード。
copy_xbool	default=True	距離を事前に計算する場合、最初にデータを中央に配置する方が数値的に正確です。copy_xがTrue（デフォルト）の場合、元のデータは変更されません。Falseの場合、元のデータが変更され、関数が戻る前に戻されますが、データ平均を減算してから加算することにより、わずかな数値の違いが生じる可能性があります。
algorithm{“auto”, “full”, “elkan”}	default=”auto”	使用するK-meansアルゴリズム。従来のEMスタイルのアルゴリズムは「full」です。「elkan」は、三角不等式を使用することにより、明確に定義されたクラスターを持つデータでより効率的です。ただし、形状の追加の配列（n_samples、n_clusters）が割り当てられるため、メモリを大量に消費します。今のところ、「auto」（下位互換性のために保持）は「elkan」を選択しますが、より良いヒューリスティックのために将来変更される可能性があります。

K-Meansの実装

irisデータセットを使ってK-Meansによるクラスタリングと可視化を行います。

まず、必要なライブラリをインポートします。

from sklearn.cluster import KMeans
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

irisデータセットを用意します。

iris = load_iris(as_frame=True)
df = iris.data

irisデータの中身を確認します。

df

index	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2

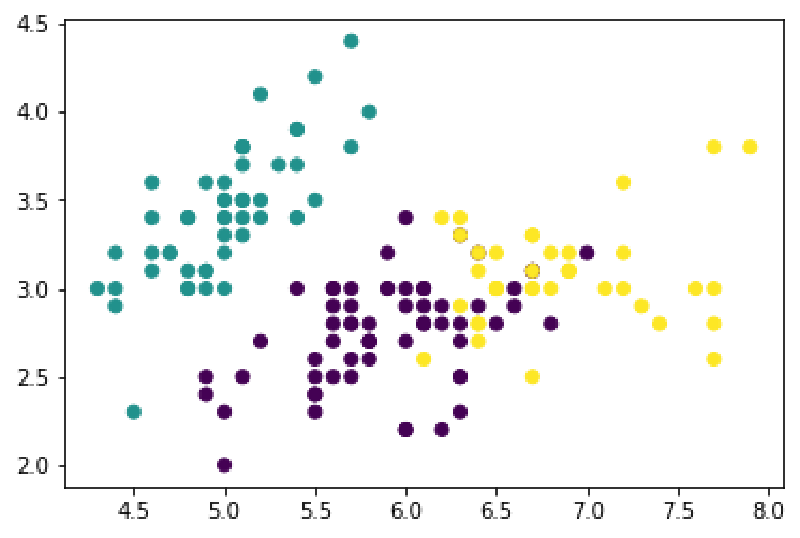
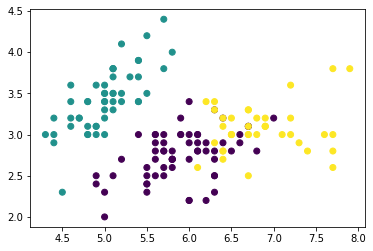
散布図を書いて可視化します。ここでは、クラスタとして3つに分けるように設定しています。

plt.scatter(df["sepal length (cm)"], df["sepal width (cm)"],  
           c = KMeans(n_clusters = 3).fit_predict(df)) 
plt.show()

K-Meansのアルゴリズムの説明と、scikit-learnでの実装についての解説は以上です。

K-Meansでクラスタリング分析の基礎を試す

scikit-learnを使用してClusteringのK-Meansを学んでいきます。